Probing Bacterial Parasitism Using Multi-Agent Reinforcement Learning
Before I begin, I need to preface this article giving credit for this project. This was the final project that my group submitted for EECS 545 and represents the work of several other graduate students: Palash Biswas, Di Chen, Adam Comer, and Niankai Yang. This project would not have been possible without the work from everyone involved. This article draws heavily from the report that was jointly written and includes diagrams and results from everyone involved. I am writing about our work not to take credit but to share our results with anyone interested.
Motivation
Bacteria in their natural environment do not exist in isolation but with several other species. Much richer dynamics can be observed with additional species. Three examples of interest include competition, commensalism, and parasitims, which are defined and illustrated in the following figure:
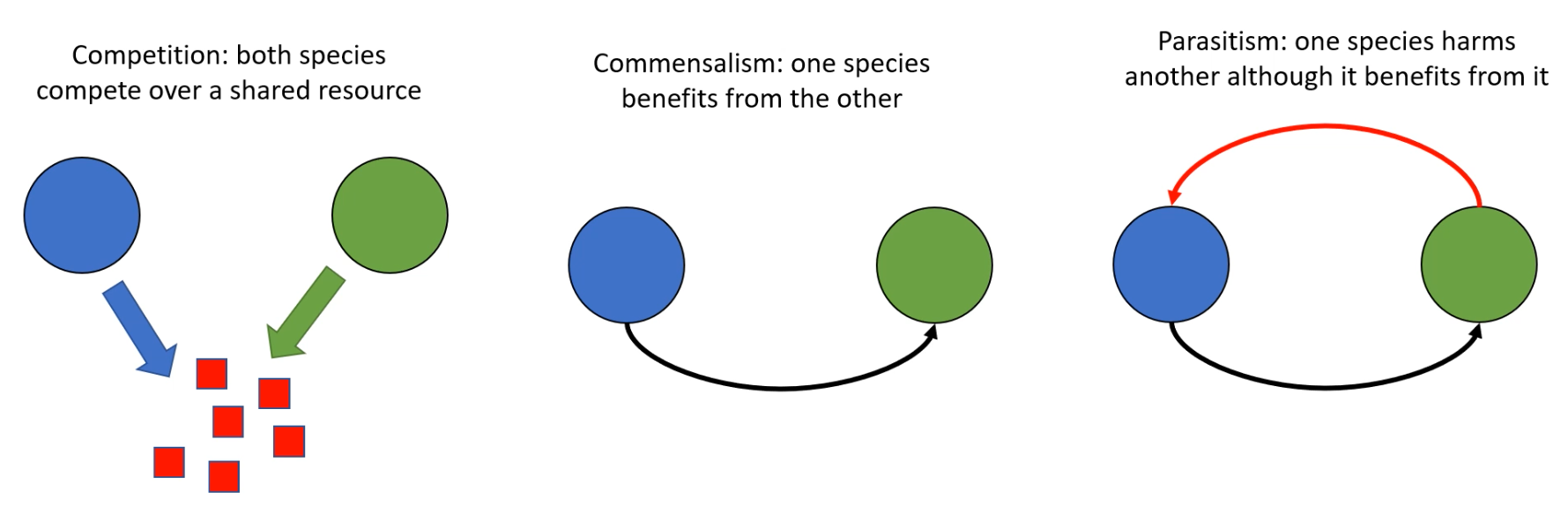 Three interactions of interest that can occur with multiple species of bacteria.
Three interactions of interest that can occur with multiple species of bacteria.
Probing these interactions is challenging, because both cooperation and competition are present1 . However, we cannot fully understand bacterial comunities without understanding these interactions.2 In this project, we use multi-agent reinforcement learning (MARL) to efficiently study these microbial interations. After the bacterial agents are trained, their optimal policies are evaluated in different environements to allow us to quantify and understand how the optimal level of antagonism varies with environmental features.
TLDR: Four minute video summarizing the project.
Background
When multiple species of bacteria exist in the same environment, we wish to know the strategies that cannot be replaced by an other strategy through natural selection. These behaviors are known as evolutionary stable strategies, and they govern the long-term behavior of bacterial communities3 . Traditionally, identifying these evolutionary stable strategies has been a problem within evolutionary game theory. However, developing tractable equations to model the dynamics among multiple bacterial species typically requires severe simplifications.
To address these shortcomings, we turn to MARL, which is concerned with agents (bacteria) finding optimal policies (evolutionary strategies) that maximize rewards (fitness) through repeated self-play. The close connection between evolutionary game theory and MARL has already been identified and established rigorously4 . To translate the the problem of identifying evolutionary stable strategies to a problem solvable with MARL, we note that the mechanism for policy exploration within MARL provides a natural mode of mutation and that rewards can be defined in a manner consistent with evolutionary fitness. Therefore, convergence of agent policies that do not change with additional training are interpeted as identifying evolutionary stable strategies within the context of the specific environment.
There exist many other techniques for simulating the evolution of bacteria. Modeling microbial population dynamics ranges from studies of gene regulatory networks with tens of thousands of kinetic action parameters governing interactions between molecules to simple differential equations governed by only a handful of parameters. With these different approaches comes an avoidable trade-off between model fidelity and computational cost. We aim to identify a class of models that is complex enough to support commensalism and parasitism but still solvable using MARL. Recent work on sequential social dilemmas by Leibo et al.5 has demonstrated the effectiveness of MARL for identifying both competitive and cooperative behaviors. However, the work of Leibo et al. was focused on larger organisms with significant cognitive capacity and environments lacking several necessary features to study bacteria specifically. Motivated by these recent findings, we developed a model of key bacteria interactions and applied MARL to identify evolutionary stable strategies as a function of the degree of parasitism and the scarcity of resources. The average rewards collected by agents represent the fitness of different evolutionary stable strategies. Note, however, that evolutionary stability does not necessarily equate to high levels of fitness, just as the Nash equilibrium of the Prisoner’s Dilemma does not lead to the highest payoff for both players.
Defining Nutrient Collection Problem
We study the behavior of two bacteria species in a 2-D environment, since this is a common ecosystem for bacteria cultures growing in agar plates and biofilms. Bacteria are able to exhibit complicated symbiotic behaviors due to their ability to sense chemical signals in their immediate suroundings through chemotaxis6 and detect nearby bacteria through quorum sensing.7 Broadly, this symbiotic relationship can be classifed as commensal, in which one species benefits from the other, or parasitic, in which one species derives benefit from the other but also harms that species. In addition to these symbiotic relationships, we assume that competition is always present, as the bacteria compete over some shared beneficial nutrients.
We base our mechanisms of commensalism and parasitism on experimental observations. Our commensal system is motivated by experimental observations that microaerophilic Campylobacter jejuni consumes nutrients more effectively in low oxgen concentrations, which are naturally produced by Pseudomonas bacteria.8, 9 Parasitism in our model is motivated by experimental observations across many species of bacteria in which one species produces metabolic byproducts that can be harmful to competing species10, 11 .
We try to capture these biological complexities in our model. We represent the different species of bacteria as two different types of MARL agents interacting in a 2-D grid world. One agent type is a host cell, which decreases the local oxygen concentration, and the other agent type is a parasite, which derives greater utility from nutrients collected in low oxygen concentrations. Both types of agents are treated as intelligent agents able to choose to move in one of the four cardinal directions informed by their partial observation of the full state of the system. Agents are able to perceive the positions of nutrients, agents, and oxygen levels about some specified radius.
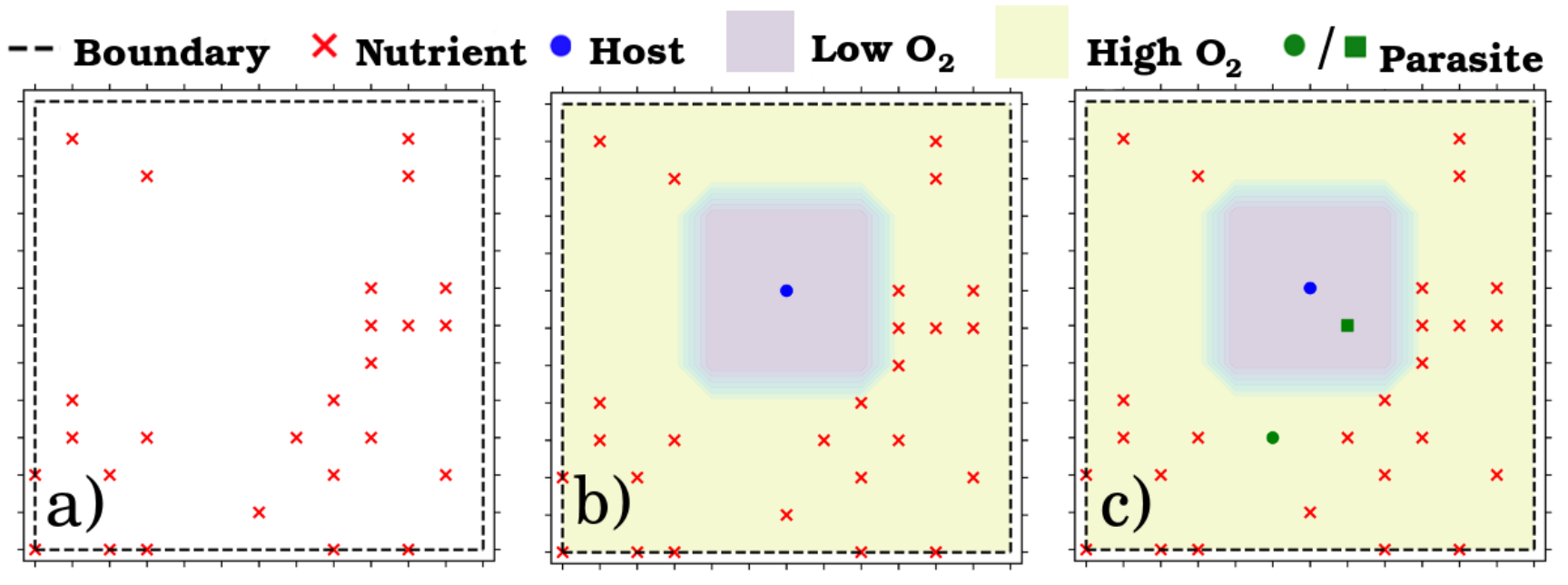 Example of an environment showing a) the distribution of nutrients, b) nutrient distribution and the host agent, along with the associated oxygen density, and c) full environment, which includes two parasites.
Example of an environment showing a) the distribution of nutrients, b) nutrient distribution and the host agent, along with the associated oxygen density, and c) full environment, which includes two parasites.
We fix many of the environmental factors across all of the experiments, but we look at three distinct classes of environments:
- We explore the effect of food scarcity by considering two different types of random nutrient distributions. In the scarce scenario, nutrients are randomly distributed throughout the environment, and the game terminates when all nutrients have been collected. In the abundant scenario, nutrients randomly regenerate, and the game terminates after some fixed number of episodes.
- We explore different sizes for the low oxygen radius centered about the host cell. This low oxygen region determines the necessary proximity of the parasitic agents to receive amplified rewards from the collected rewards.
- We explore variable degrees of parasitism severity by adding a “deactivation zone” about the host cell. We assume there exists some zone of specified radius about the host cell that deactivates the host for the following timestep if both parasitic agents are in the deactivation zone. This zone models a threshold concentration of parasitic metabolic byproducts that is exceeded when too many parasites are near the host and induces paralysis.
We can now characterize our toy system using the framework of evolutionary game theory. Without a deactivation zone, the system is commensal (with competition), but the deactivation zone makes our system parasitic (with competition). The severity of the parasitism is determined by the relative magnitude of the low oxygen radius and the deactivation zone radius. For convenience, we define the following labels describing the severity of parasitism:
| Degree of Parasitism | Low Oxygen Radius | Deactivation Radius |
|---|---|---|
| Mild Commensalism | 2 | – |
| Moderate Commensalism | 4 | – |
| Mild Parasitism | 4 | 2 |
| Moderate Parasitism | 2 | 2 |
| Severe Parasitism | 4 | 4 |
Finally, we explore how the behaviors of the different agents under varying degrees of parasitism are affected by the nutrient scarcity.
Solving the Nutrient Problem with MADDPG
We treat the nutrient collection problem as a Markov decision process that can be solved using MARL. Specifically, we use multi-agent deep deterministic policy gradients (MADDPG), which have been shown to outperform the more common deep Q-networks in mixed cooperative and competitive environments.12
This algorithm is a multi-agent variant of the actor-critic algorithm DDPG. Two neural networks are used to parameterize the policy $\pi^{(i)}$ and value functions $Q^{(i)}$, respectively. The expressions for maximizing the expected cumulative rewards come from the policy network, and the value network is updated using Q-learning.
Although DDPG works well for reinforcement learning with a single agent, it suffers from high variance in the gradient used for updating the policy network. With multiple agents, the problem of high variance is amplified by the fact that the rewards received by the agent are also conditioned upon the actions of other agents. For this reason, the MADDPG algorithm formulates the value fuction not only as a function of the observations and actions of the respective agent but as a function of the the observations and actions of all of the agents. This is known as centralized training, since it requires knowledge available to all agents. During execution, however, only the actor is used. This decentralized execution allows MADDPG to improve the training stability without imposing unrealistic assumptions on the agent policies.
Both the policy and value neural networks were kept small, due to the simplicity of the environment. The networks had a single hidden layer of 64 nodes, and deepening the network did not increase agent performance. However, we briefly looked into approximating the policy and value functions using both convolutional neural networks and convolution recurrent neural networks, since these implementations better capture the temporal and spatial information to inform more intelligent policies. Although agents using these architectures performed better than those using fully-connected neural networks, we did not have the computational means to systematically perform all of the necessary experiments. For this reason, I will only cover our results from the fully-connected networks here.
With such simple networks, the architectures are largely uninteresting. However, we did find that the network performance was improved using the Gumbel-Softmax estimator, which converts the continuous output from the neural networks into one-hot vectors.13 The Gumbel-Softmax estimator can lead to more accurate gradient estimates in our policy network because it permits performing the chain rule when converting to a discrete action space.
The principal quantity of interest is the score of each agent, which is determined by not only the nutrients collected but also the local oxygen concentration at the time of collection for the microaerophilic parasitic agents. When two agents land on the same nutrient, it is evenly split between the agents. We can look at the scores collected by the agents to determine when the policies converge. Below, we plot the training curves obtained for all three agents under moderate parasitism for all three agents with both scarce nutrients and abundant resources. We note that the rewards have stabilized after around 4000 episodes, 800 of which were performed randomly to populate the buffer of each agent.
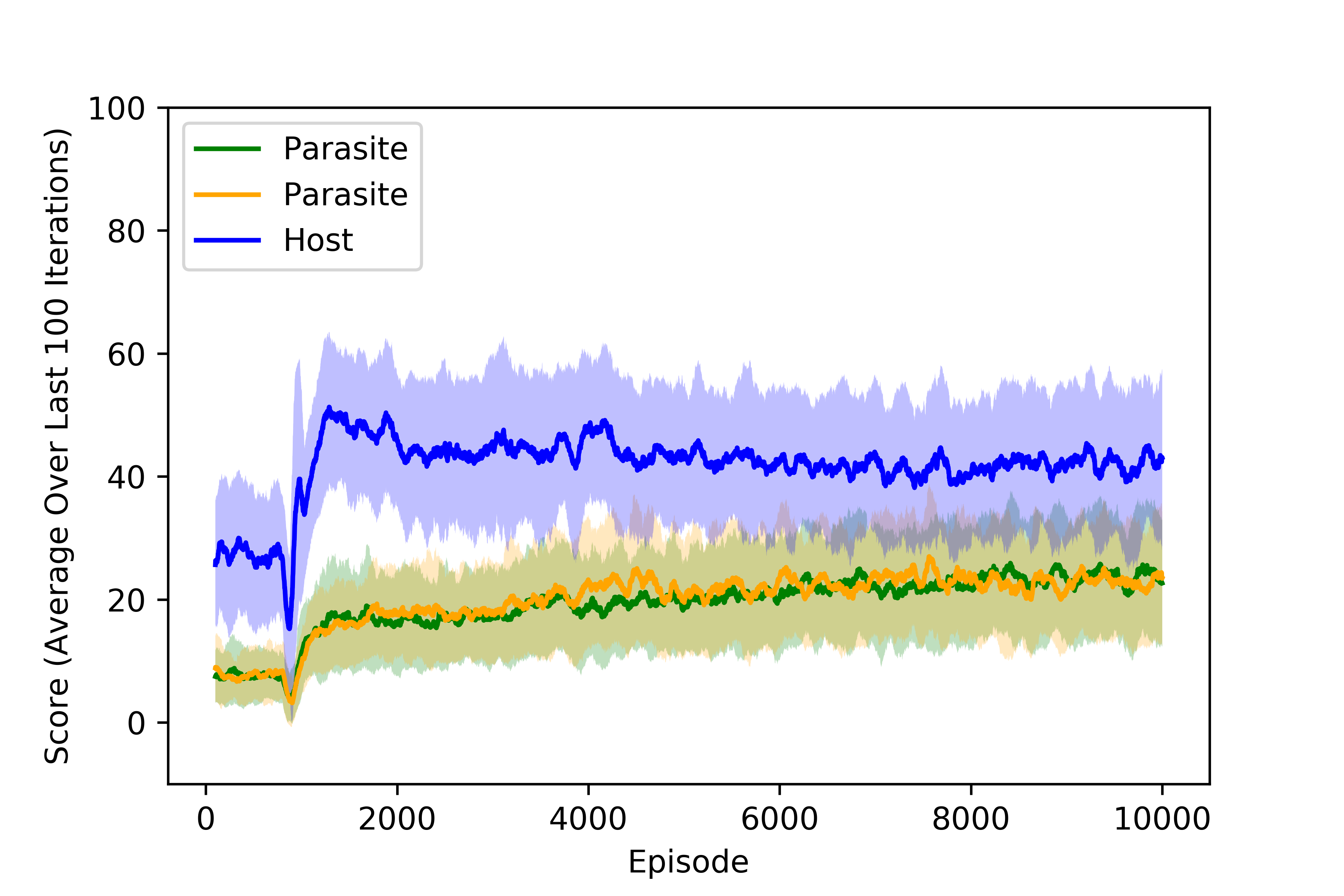 Training curves for agents trained under moderate parasitims with scarce resources.
Training curves for agents trained under moderate parasitims with scarce resources.
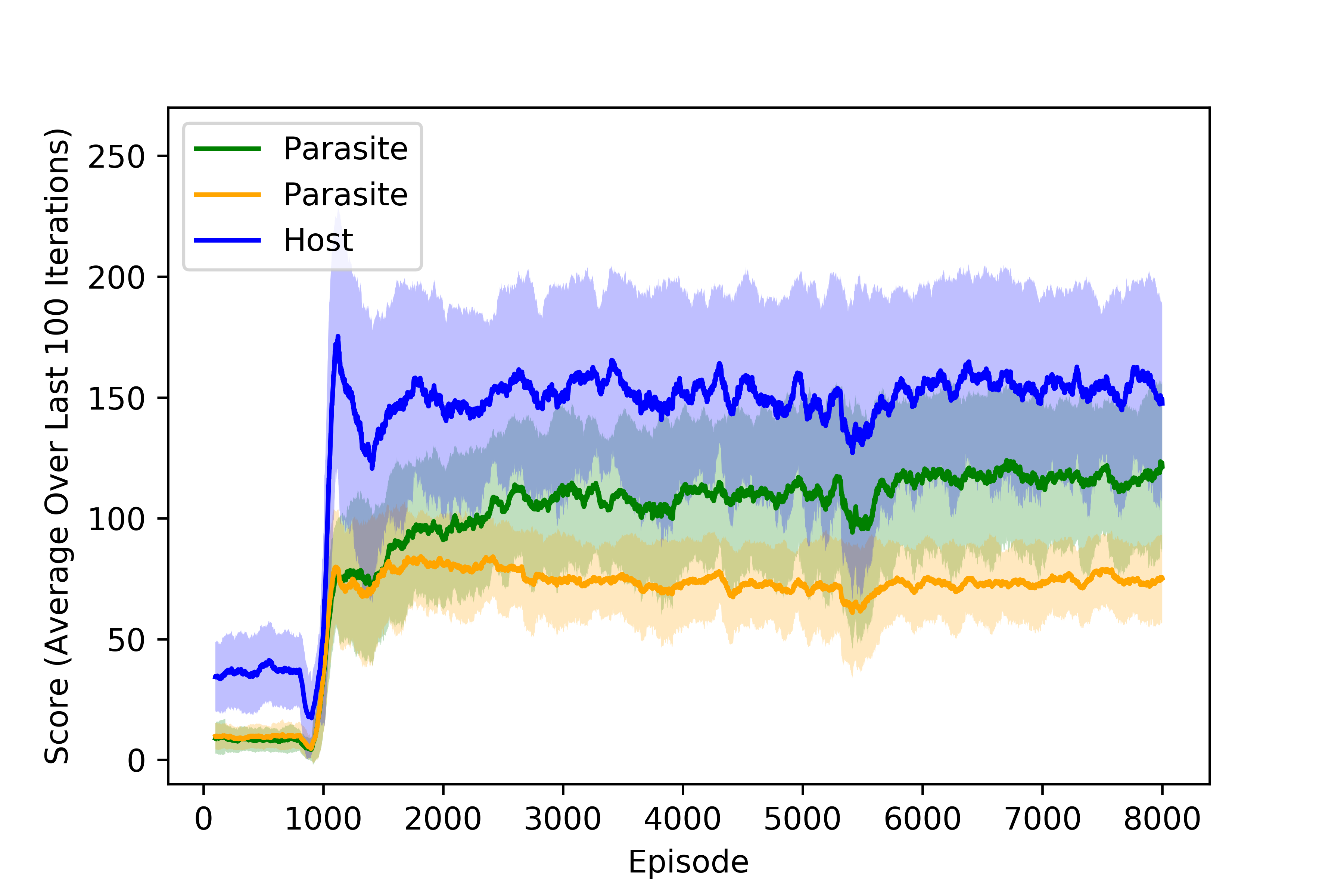 Training curves for agents trained under moderate parasitims with abundant resources.
Training curves for agents trained under moderate parasitims with abundant resources.
Examining Trained Agents
Visualizing Training
Although the agent scores are the chief quantity of interest, there are a number of interesting features we can examine using the trained agents. First, and most basic, we can evaluate the policies of the agents at different points during the training. We will look at the system with scarce resources under severe parasitism. The evolution in policies is interesting with parsitism because, as we will see, the parasites first learn to antagonize the host cell before finally reducing their level of antagonism to allow more nutrients to be collected. In the videos below, we represent the deactivation zone using a dashed grey line surrounding the host cell.
First, we can look at the evaluated policies after 500 episodes. At this point in the training, the agents are behaving randomly to fill up their buffer with training data.
Next, we look at our agents after 1500 episodes. We see that the parasites are learning to strategically deactivate the host to gather more nutrients for themselves. However, the parasites are too aggressive, in the sense that that the host is unable to explore the entire environment, preventing the parasites from achieving maximal rewards for each nutrient.
Finally, we look at the well-trained agents after 4500 episodes. Now the parasites have learned to reduce their level of antagonism so that all of the rewards can be collected. Note that we consider this policy optimal because additional training does not improve the results, not because one cannot imagine a slightly different strategy allowing more rewards for any particular agent.
Comparing Learned Policies
With a sense of how the policies converge during training, we can now compare the learned policies across different levels of parasitism. Before we do this quantitatively, it is instructive to simply visualize the policies of the agents learned under different levels of parasitism.
First, we look at the mild commensalism case. There is no deactivation zone, but the parasites still benefit from collecting nutrients in the low oxygen region. For this reason, we see that all three agents tend to stick together, often all occupying the same same grid point. This video illustrates the strong level of cooperation that can be achieved in our simple system.
Next, we can look at the system with mild parasitism. The low oxygen radius has increased to 4 gridpoints, and there is now a deactivation radius of 2 grid points. The parasites stay within the low oxygen region created by the host cell, but they rarely deactivate it. In the first half of the video, one can see the host cell attempting to flee from the parasites and gain as many nutrients as possible. After the parasites have caught up to the host, they can manipulate its trajectory to prevent it from gathering the remaining rewards.
Finally, we look at the system under severe parasitism. The low oxygen region has now been reduced to the same size as the deactivation region. The parasites must now follow the host cell much more closely than with mild parasitism, and they frequently utilize deactivating the host.
Characterizing Host and Parasite Fitness
We look at the mean collected rewards of both the host and parasite with stable policies, and we interpret this to be analogous to biological fitness. Similar to what was suggested in the training videos above, we observe that the fitness of the hosts and parasites is a non-monotonic function of parasitism severity, suggesting that the optimal level of parsitism to maximize rewards is neither maximally nor minimally parasitic, even for the parasitic agents. This relationship also depends on the scarcity of resources.
Scarce Resources
We first look at the fitness of the parasite and host cells with scarce resources. In the figure below, we see that the fitness of the host strictly decreases with parasitism severity. As the parasitic agents become more aggressive, the host cell becomes further confined by the parasites and gathers fewer nutrients. The fitness of the parasitic agents exhibits a more complicated relationship with the parasitism severity. Somewhat counterintuitively, the parasites can be adversely affected by a deactivated host even though they are competing for resources with the host cell. If the host cell is deactivated too frequently, the parasites are unable to collect all of the possible nutrients inside a low oxygen concentration.
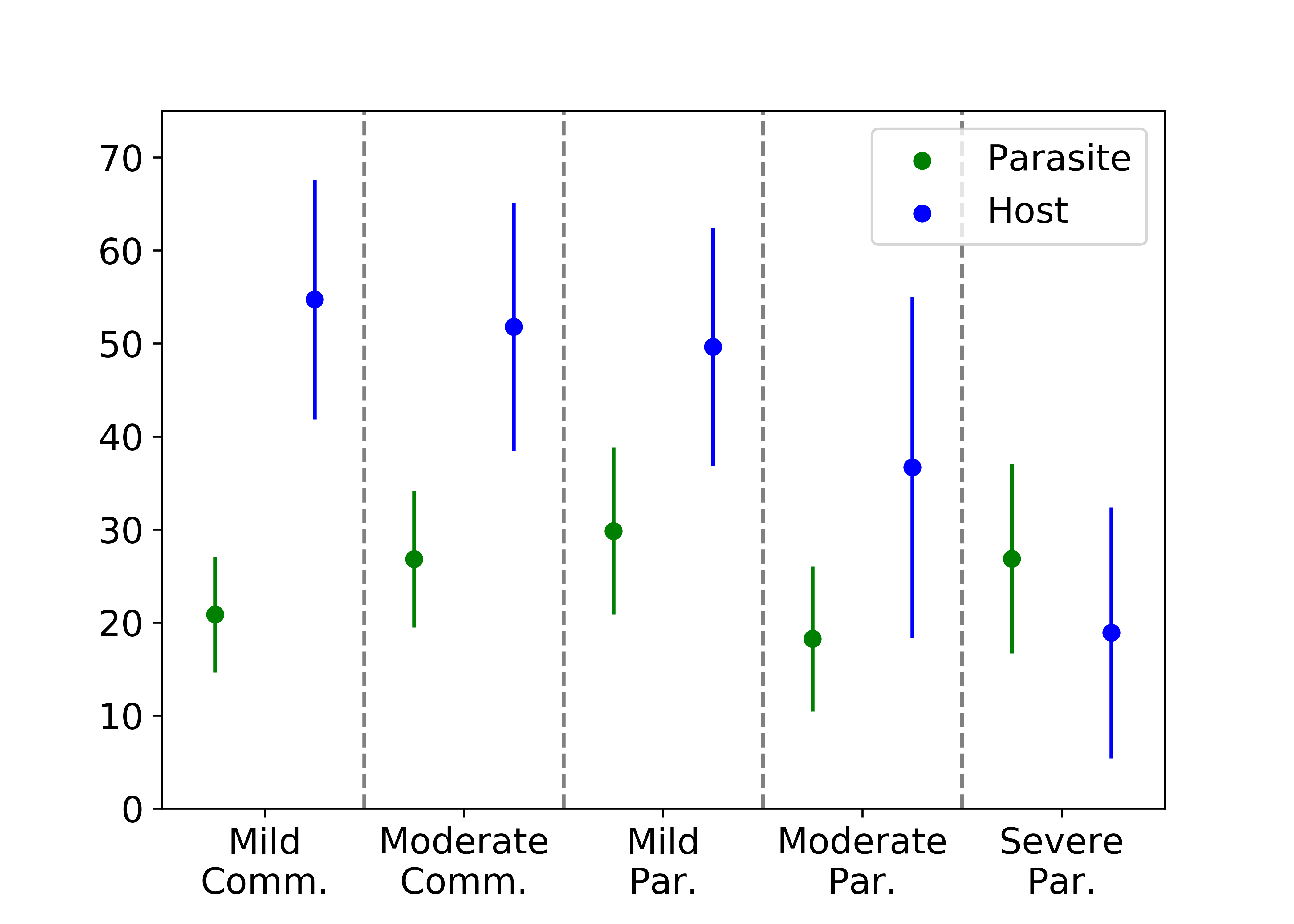 With scarce resources, the host cell collects fewer rewards with increasing parasitism severity while the relationship of the rewards collected by the parasites is more complicated.
With scarce resources, the host cell collects fewer rewards with increasing parasitism severity while the relationship of the rewards collected by the parasites is more complicated.
In examining the number of nutrients collected, we find that the parasites collect roughly the same number of nutrients across all levels of parasitism. The difference in fitness is caused by the whether the nutrients were collected in a low oxygen region and also the number of split rewards. In the plot below, we see that when the low oxygen region is enlarged, the parasitic cells are able to collect nutrients more easily in the low oxygen region without having to share them. This helps explain the curious trend observed in the parasite fitness. Finally, it is worth noting that the fitness of the parasites relative to the host increases monotonically with parasitism, as we would expect.
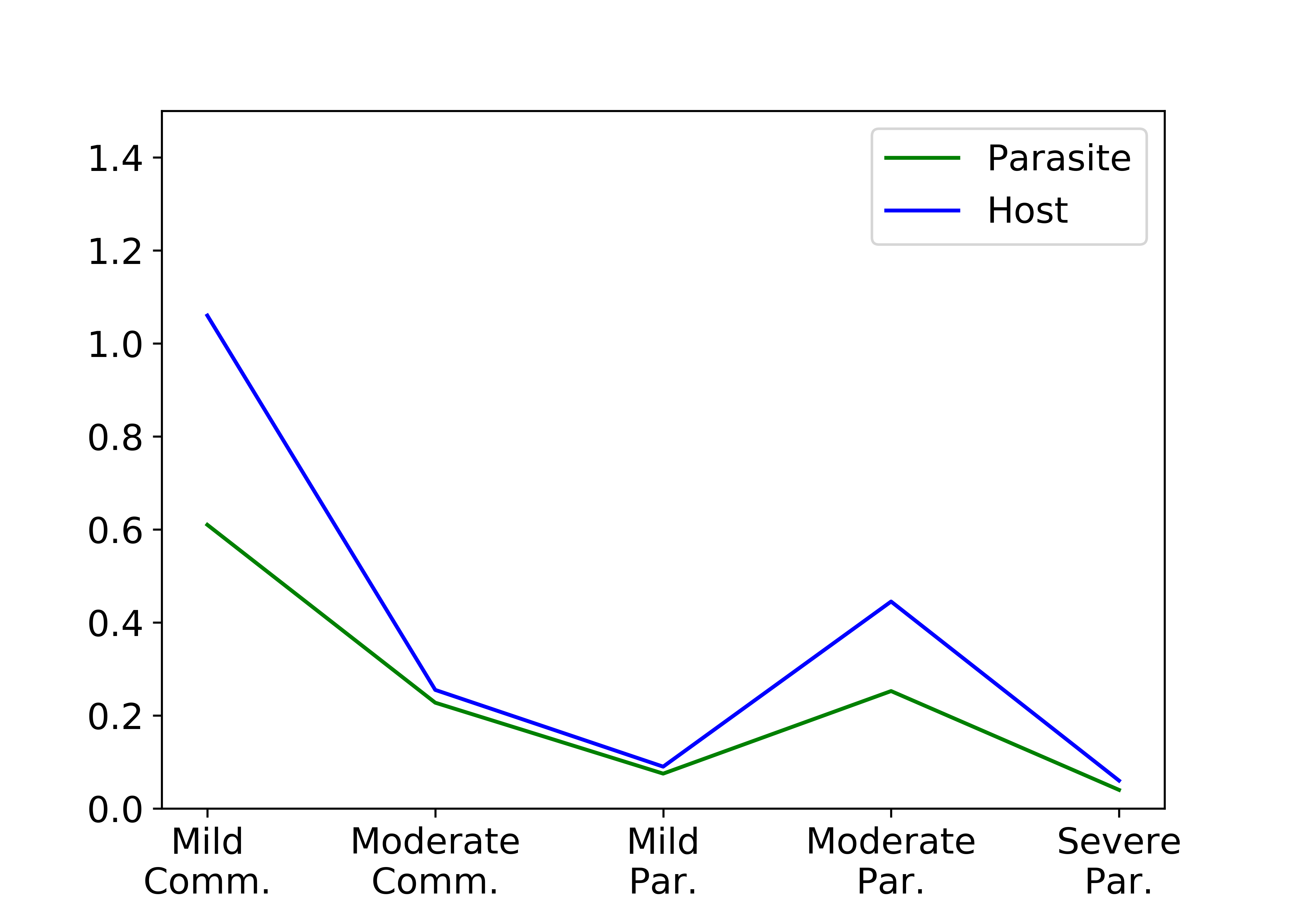 The number of split rewards depends strongly on the size of the low oxygen region, which incentivizes the parasites to be in close proximity to the host cell.
The number of split rewards depends strongly on the size of the low oxygen region, which incentivizes the parasites to be in close proximity to the host cell.
 The relative fitness of the parasite cell increases with increasing parasitism, as we would expect.
The relative fitness of the parasite cell increases with increasing parasitism, as we would expect.
Abundant Resources
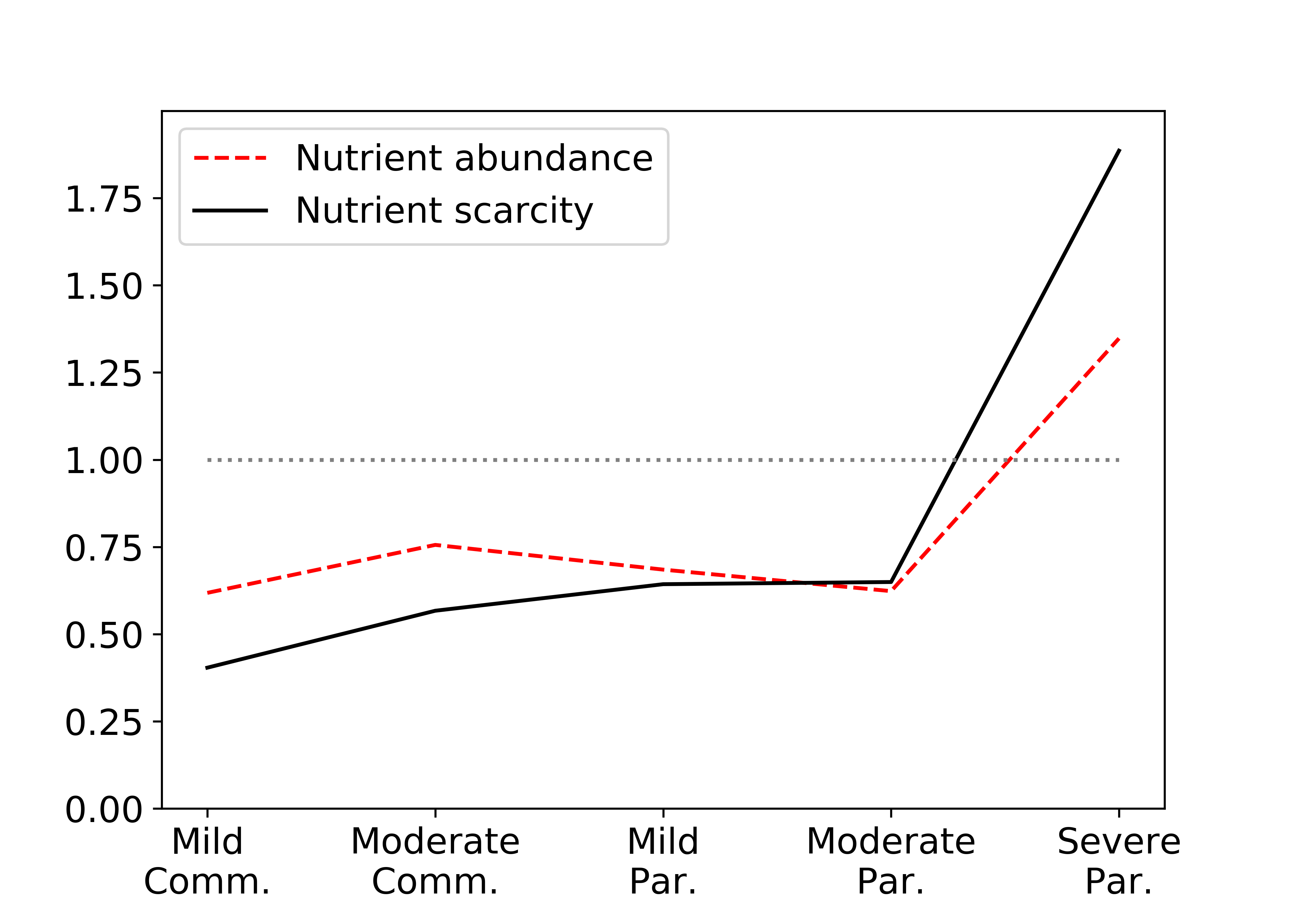
We observe qualitatively different results with abundant, regenerating nutrients. Interestingly, we see in the figure below that the host fitness initially increases with parasitism before dropping off sharply. This difference from the scarce environment is due to the overall reduction in competition for rewards. In going from mild to moderate commensalism, for instance, the low oxygen region grows, and the parasitic agents are less likely to compete with the host agent over rewards. We also observe that the parasites now implement a new strategy at times. One parasite remains new the host agent to collect the nutrients at a higher reward, while the other parasite ignores the low oxygen region entirely to find a region of high nutrient density without any competition pressure. Evidence of this behavior is seen in looking at the number of times the host cell is deactivated as a function of parasitism, and this effect can also be seen in looking at the number of split rewards with abundant resources.
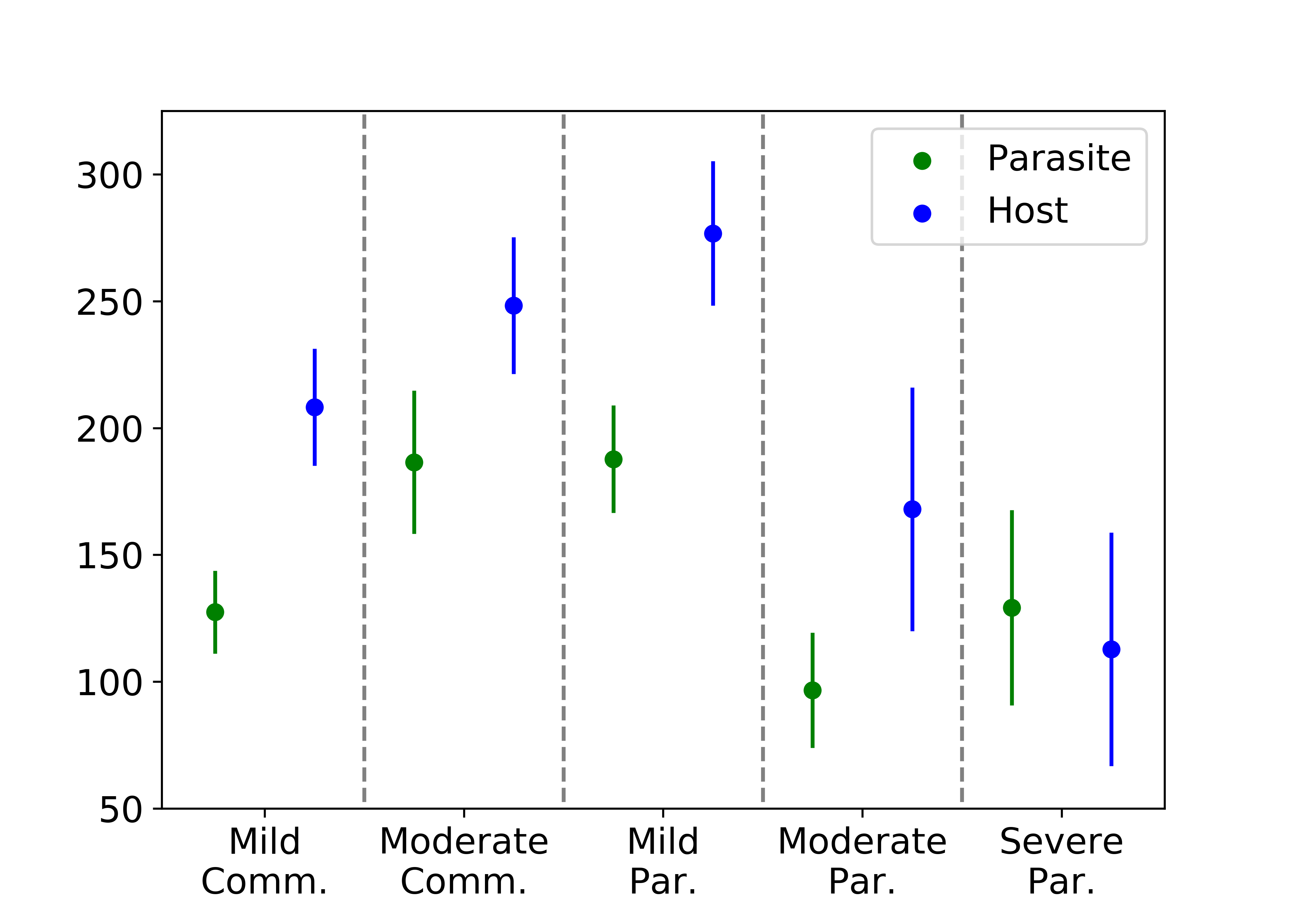 With scarce resources, the host cell collects fewer rewards with increasing parasitism severity while the relationship of the rewards collected by the parasites is more complicated.
With scarce resources, the host cell collects fewer rewards with increasing parasitism severity while the relationship of the rewards collected by the parasites is more complicated.
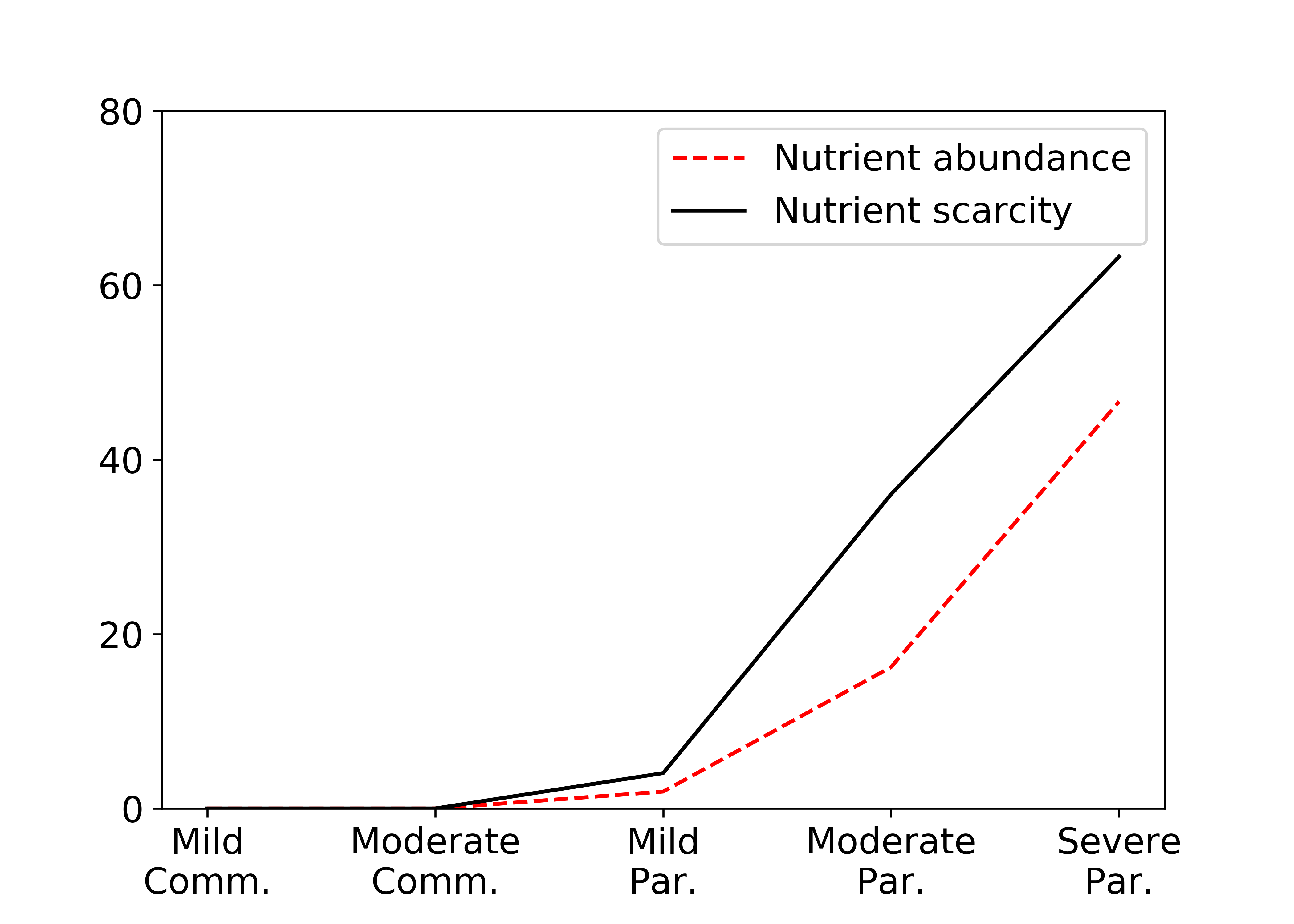 While the host is always deactivated more with increasing parasitism severity, the effect is reduced with abundant resources.
While the host is always deactivated more with increasing parasitism severity, the effect is reduced with abundant resources.
Importance of Centralized Training
We also wanted to evaluate the utility of centralized training for agents in our specific environment. For this reason, we also trained all of the agents separately using DDPG, which does not use centralized training but instead relies on only the observations and actions of the respective agent. All models were trained for 3200 epochs, and the trained policies were evaluated over 100 iterations on random initial positions.
We observe the in environments ranging from mild commensalism to mild parasitism, the total scores obtained by summing the rewards of all three agents are higher with MADDPG compared to DDPG. This observation reinforces the importance of a centralized critic the success of multi-agent reinforcement learning. However, for the environments with moderate and severe parasitism, the decentralized DDPG leads to higher total scores. Looking more carefully, we see that the host cell obtains greater rewards in these settings using DDPG compared to the rewards it obtained using MADDPG. We believe that the DDPG-trained policies result in fewer deactivations of the host, and the added mobility of the host cell permits larger scores for the entire ecosystem. However, this does not mean that the DDPG policy is necessarily a better analogue of the underlying evolutionary stable strategy.
| Degree of Parasitism | MADDPG Total Score | DDPG Total Score |
|---|---|---|
| Mild Commensalism | 96.68 | 90.08 |
| Moderate Commensalism | 105.40 | 99.30 |
| Mild Parasitism | 109.09 | 102.35 |
| Moderate Parasitism | 73.03 | 74.52 |
| Severe Parasitism | 72.50 | 79.37 |
Video Summary
We recorded a short video on our project as part of our course submission. It briefly covers the model we developed for exploring the degree of parasitism, using MARL to evolve the policies of the agents, and a handful of our results.
Conclusion
To date, this present study represents the first effort known to us to apply MARL with environmental conditions, reward structures, and agent perceptions specific to microbial interactions and to interpret the results in terms of bacterial interactions. We applied MARL through MADDPG to converge approximations to evolutionary stable strategies exhibiting behaviors consistent with specific bacteria interactions in the microbiology literature (e.g., C jejuni and Pseudomonas commensalism). We examined the effects of resource scarcity and degrees of parasitism in a toy model of evolution.
In environment with scarce resources, we found that the host fitness declines with increased parasitism, as expected. However, parasite fitness reaches a maximum at intermediate levels of parasitism, providing insights into the delicate balance parasites must strike between their own fitness and that of the host. More complex dynamics were observed for the host under abundant nutrients, since competition in a local region was less critical. The trends of parasite fitness were consistent across both scarce and abundant environments, but the parasites engaged in antagonism less often in abundant environments.
Finally, we investigated multiple network architectures to serve as the approximators for the policy and value functions within MADDPG, and we found that the fully-connected architecture significantly reduced training time compared to more complicated architectures with only slightly worse performance. We also performed an abalative study of the centralized training, the distinguishing feature of MADDPG compared to DDPG. We found that for the limited environments tested, centralized training provided only a modest benefit, suggesting that our results are robust to algorithmic change.
Accompanying Code
Because the code for this project represents the combined work of several people, I am not making it publicly available.
References
- S. Hummert, et al. “Evolutionary game theory: cells as players." Molecular BioSystems, 10.12: 3044-3065, 2014.
- J. Overmann and H. van Gemerden. “Microbial interactions involving sulfuric bacteria: implications for the ecology and evolution of bacterial communities." FEMS Microbiology Reviews, 24.5: 591-599, 2000.
- C. C. Cowden. “Game Theory, Evolutionary Stable Strategies and the Evolution of Biological Interactions." Nature Education Knowledge, 3(10):6, 2002.
- K. Tuyls and A. Nowé. “Evolutionary Game Theory and multi-agent reinforcement learning." Knowledge Engineering Review, 20(1):63-90, 2005.
- J. Z. Leibo, et al. “Multi-agent reinforcement learning in sequential social dilemmas." Proceedings of the International Joint Conference on Autonomous Agents and Multiagent Systems, AAMAS, 1:464-473, 2017.
- P. Singleton. Bacteria in Biology, Biotechnology and Medicine. John Wiley & Sons, 6th edition, 2004.
- M. B. Miller and B. L. Bassler. “Quorum Sensing in Bacteria." Annual Review of Microbiology, 55:165-199, 2001.
- F. Hilbert, M. Scherwitzel, P. Paulsen, and M. P. Szostak. “Survival of Campylobacter jejuni under conditions of atmospheric oxygen tension with the support of Pseudomonas spp." Applied and Environmental Microbiology, 76(17):5911-5917, 2010.
- J. C. Kim, E. Oh, J. Kim, and B. Jeon. “Regulation of oxidative stress resistance in Campylobacter jejuni, a microaerophic foodborne pathogen." Frontiers in Microbiology, 6:751, 2015.
- H. K. Kuramitsu, X. He, R. Lux, M. H. Anderson, and W. Shi. “Interspecies interactions within oral microbial communities." Microbiology and Molecular Biology Reviews, 71(4):653-670, 2007.
- M. Heil. “Host manipulation by parasites: Cases, patterns, and remaining doubts." Frontiers in Microbiology, 6:751, 2015.
- R. Lowe, Y. Wu, A. Tamar, J. Harb, O. P. Abbeel, and I. Mordatch. “Multi-agent actor-critic for mixed cooperative-competitive environments." Advances in neural information processing systems 6379-6390, 2017.